3. 공정 능력 정의, 미니탭, R, 파이썬으로 분석
공정능력 정의
공정능력은 “Process가 안정된 상태에서 양품을 생산할 수 있는 능력”으로 정의할 수 있다. 이는 어떤 부품을 납품받거나 협력사의 공정을 점검할 때 필수적으로 확인하는 항목으로, 제품이나 공정의 종류와 관계없이 규격 대비 산포가 어떤지, 예상 불량률이 어느 정도인지 한눈에 파악할 수 있는 유용한 지표이다.
협력사의 공정을 점검할 때, 주요 관리 항목들의 공정능력 현황과 개선이 필요한 항목들만 살펴보아도 해당 제조 라인의 운영 수준을 대략적으로 파악할 수 있다.
공정능력은 산포를 계산하는 방식에 따라 단기 공정능력과 장기 공정능력으로 구분되며, 보통 단기 공정능력은 공정이 안정된 짧은 기간의 데이터를 바탕으로 하고, 장기 공정능력은 전체 공정의 안정성과 이상 여부까지 반영한다.
규격 상한만을 고려할 때의 공정능력은 CPU, 규격 하한만을 고려할 때는 CPL이라고 표현한다. 상하한을 모두 고려한 종합적인 공정능력을 나타내는 지표는 Cpk이며, 이는 공정 평균이 규격 중앙에서 얼마나 벗어나 있는지를 반영한 값이다. 따라서 Cpk는 실제 공정이 어느 정도 품질 수준을 유지하고 있는지를 보다 정확히 평가할 수 있는 지표로 활용된다.
공정 능력 계산 시에는 관리도의 관리 상하한을 벗어난 이상치를 제외하고 계산해야 한다. 이는 공정 능력이 ‘공정이 안정된 상태에서 양품을 생산할 수 있는 능력’을 의미하기 때문이다. 대부분의 프로그램은 이상치를 포함한 데이터를 기준으로 계산하지만, 엄밀한 분석을 위해서는 이상치를 제거한 후 공정 능력을 재계산하는 것이 바람직하다.예를 들어, 어떤 공정의 평균 처리 시간이 약 30초이며 군내 표준편차가 1.5인 경우, 대체로 Cp 값이 1.5 이상으로 안정된 공정으로 판단된다. 하지만 특정 샘플(예: 10번째 샘플)에서 50초라는 극단적인 이상치가 포함되면 전체 표준편차가 크게 증가하면서 Cp 값이 1.0 이하로 낮아질 수 있다. 이 경우 공정능력이 과소평가되며, 실제보다 공정이 불안정하다고 판단될 수 있다. 따라서 이상치를 식별하고 제거한 뒤 재계산하는 것이 정확한 공정 능력 평가를 위해 매우 중요하다
공정능력 계산
Cp (단기공정능력)
공정의 산포가 규격 범위 내에 얼마나 들어맞는지를 평가. 공정의 중심 위치는 고려하지 않는다.
- USL: 상한 규격 (Upper Specification Limit)
- LSL: 하한 규격 (Lower Specification Limit)
- σ (시그마): 공정의 표준편차 (산포)
Cpk (중심치를 고려한 공정능력)
산포의 중심을 고려하여 계산 할 때, Cp와 Cpk값을 같이 비교해 보아야 한다.
여기서 사용된 시그마(σ)는 군내 산포(Within-group variation)로 계산된 것으로 다음과 같이 결정된 것이다.
시그마의 계산은 Rbar/d2 계수 또는 sbar로 계산할 수 있다.
Pp, Ppk (장기 공정능력)
공정의 장기적인 변동(군간 산포를 포함한)은 모든 데이터의 표준 편차로 직접 계산한다. 이때 단기 공정능력과 구분하기 위해서 Pp, Ppk라고 표현한다.
개별 측정치
전체 평균
샘플 개수
✅ 공정능력지수 (Cp, Cpk) 판단 기준
공정능력지수(Capability Index)는 생산 공정이 규격(USL, LSL) 내에서 얼마나 안정적으로 운영되는지를 나타내는 지표입니다. 아래는 Cp 및 Cpk 값에 따른 공정 상태 판단 기준입니다.
| 공정능력지수 (Cp, Cpk) | 판단 기준 |
|---|---|
| Cpk < 1.0 | 불량이 발생 할 수 있는 공정, 특히 중심치가 벗어나면 불량이 증가 할 수 있는 수준 |
| 1.0 ≤ Cpk < 1.33 | 경계선 공정 (규격 내 운영 가능하나 개선 필요) |
| 1.33 ≤ Cpk < 1.67 | 적절한 공정 (대부분 제품이 규격 내에 있음) |
| Cpk ≥ 1.67 | 우수한 공정 (품질 관리가 잘된 상태) |
| Cpk ≥ 2.0 | 6시그마 수준의 공정 (거의 모든 제품이 규격 내에 존재) |
- 일반적으로 Cp 또는 Cpk가 1.33 이상이면 품질이 양호한 것으로 판단됩니다.
- 자동차, 반도체 등의 정밀 산업에서는 1.67 이상을 요구하는 경우가 많습니다.
- Cp와 Cpk의 차이가 크면 공정 평균이 규격 중심에서 벗어나 있다는 의미입니다.
공정 능력 지수가 1 미만이면 공정 능력이 부족하다고 판단하고, 0.67이하이면 시급히 개선해야 한다고 판단한다.
실제로 부품이나, 공정 관리를 해보면 1정도의 수준만 나와도 예상 불량율이 0.27% 수준으로 높다고는 할 수 없으나 중심치 움직이면 생기면 대규모 불량이 발생 할 수 있기에 1.33 또는 1.67정도의 공정능력을 요구하는 것이다.
신제품, 신규 공정 도입시에는 달성하기 쉽지 않은 공정 능력 수준으로 개발 단계부터 적절한 생산 능력을 감안한 규격이 설계되어야 할 것이다.
미니탭으로 분석
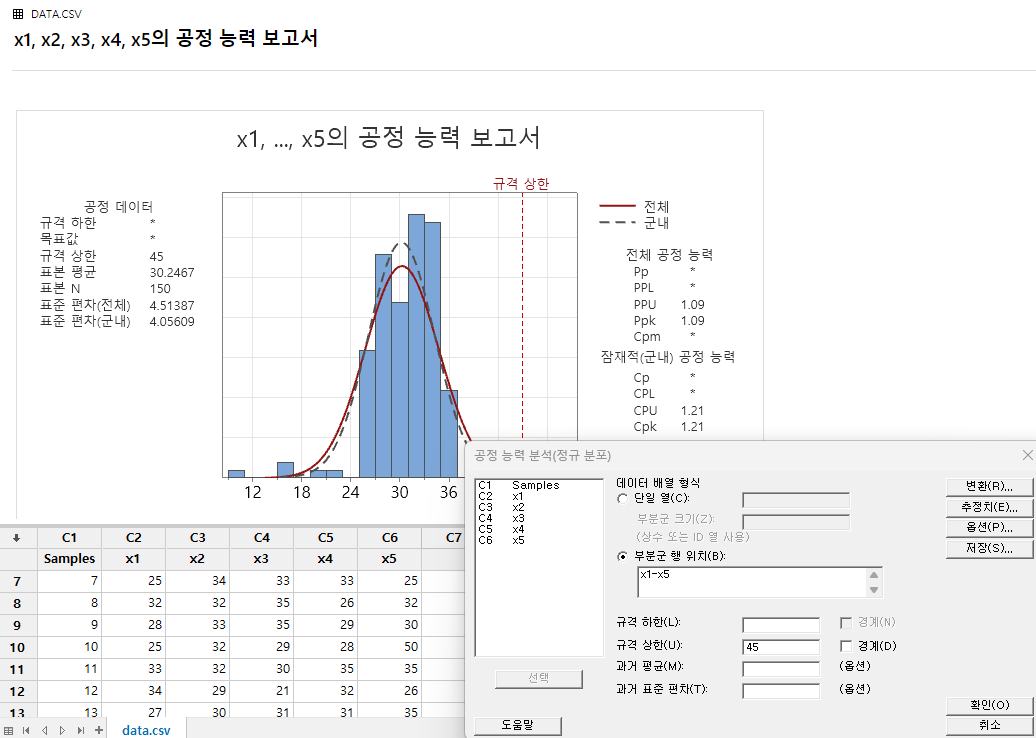
병원 입원 환자 처리 시간으로 미니탭으로 공정 능력을 계산해 보았다. 이때 Spec은 45초 이상 소요되면 고객 불만이 제기 될 수 있기에 가상으로 설정해 보았다.
미니탭 매뉴에서 통계분석>품질 도구> 공정능력 분석>정규분포를 선택하였다. 추정치에서 Sbar를 사용하여 계산하였다.
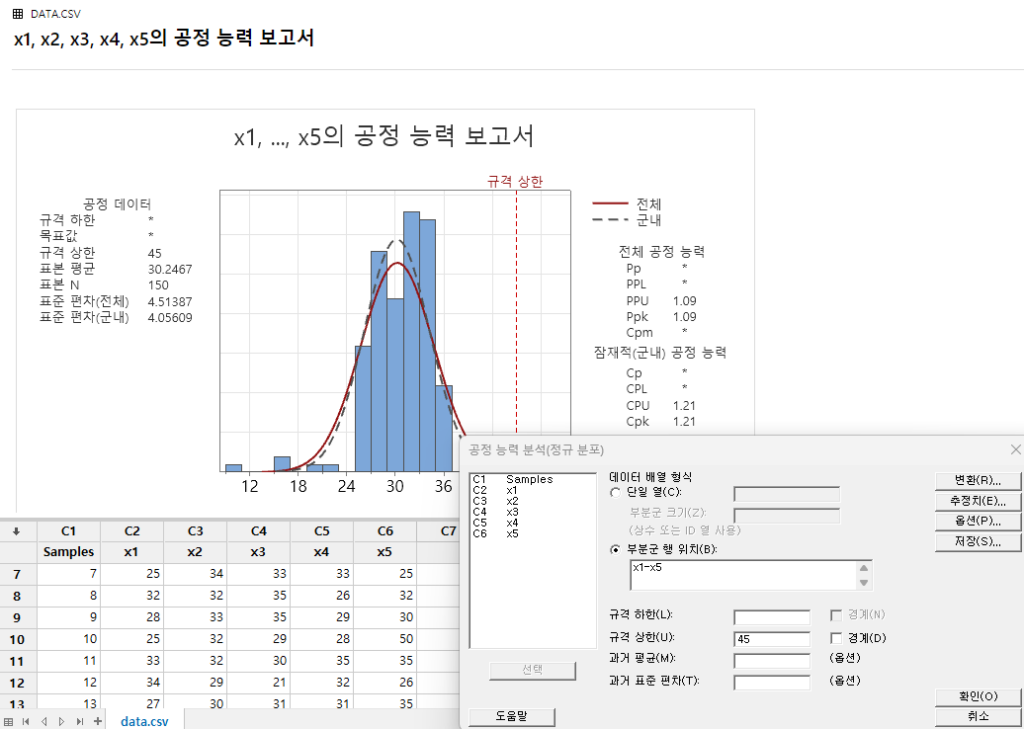
단기 공정능력(CPU)은 1.21, 장기 공정능력(PPU)은 1.09로 나타난다. 평균 처리 시간은 30초이며, 군내 표준 편차는 1.37, 군간 표준 편차는 4.39, 전체 표준 편차는 4.67 수준이다. 또한, 10번째 샘플에서 50초 데이터가 1개 존재하는 것을 확인할 수 있다.
공정 관리에서는 공정능력지수를 확인하는 것뿐만 아니라, 군내 및 군간 표준 편차를 분석하고 샘플 간 편차를 검토하여 군내, 군간 산포 모두 보며 관리 하 것이 중요하다.
R로 분석
R로 분석하는 방법은 SPC에서 사용한 qcc 패키지를 활용 하면 쉽게 분석 할 수 있다.process.capability()는 qcc 객체를 기반으로 하기 때문에 반드시 먼저 qcc()를 실행해야 합니다
실행 할 때 std.dev 계산하는 방식이 범위를 기반으로 하는 계산에는 “”UWAVE-R”을 샘프의 표준편차의 평균으로 계산 할 때는 “UWAVE-SD”라는 옵션을 입력해야 한다.
qcc에서는 단기 공정 능력만 제공하기 때문에 장기 공정 능력은 전체 데이터로 표준편차를 별도로 계산하여 그려야 한다.
> # 데이터 읽기
> data <- read.csv("D:/spc_blog/data.csv", row.names=1)
> library(qcc)
> # 데이터 Spec 설정
> USL <- 45
> # 평균 관리도 작성하며, 산포 계산
> q <- qcc(data, type = "xbar", std.dev = "UWAVE-SD")
> # 공정 능력 계산
> cap <- process.capability(q, spec.limits = c(NA, USL))
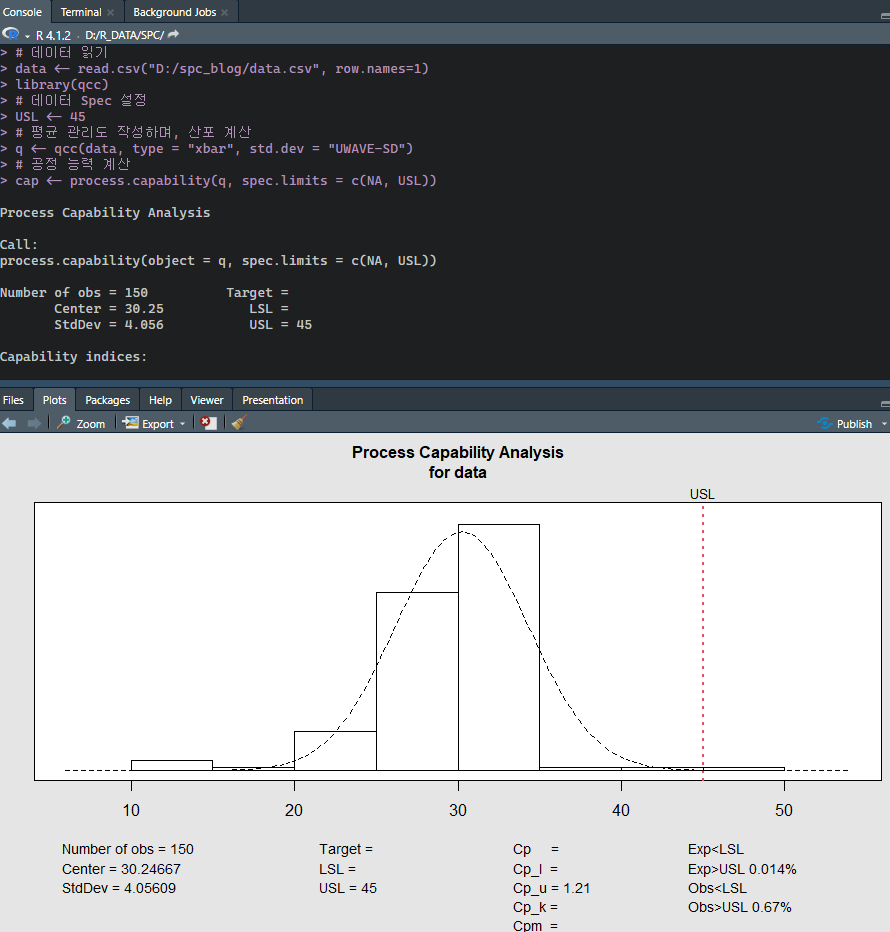
Process Capability Analysis
Call:
process.capability(object = q, spec.limits = c(NA, USL))
Number of obs = 150 Target =
Center = 30.25 LSL =
StdDev = 4.056 USL = 45
Capability indices:
Value 2.5% 97.5%
Cp
Cp_l
Cp_u 1.212 1.089 1.336
Cp_k
Cpm
Exp<LSL Obs<LSL Exp>USL 0.014% Obs>USL 0.67%
> # 전체 평균_수치형으로 변환 내역 입력력
> x_bar <- mean(as.matrix(data))
> # 전체 표준편차 (장기 산포)
> sigma_overall <- sd(as.matrix(data))
> Ppu <- (USL - x_bar) / (3 * sigma_overall)
> Ppu
[1] 1.089482
> # 장기 공정 능력 게산
> Ppu <- (USL - x_bar) / (3 * sigma_overall)
> Ppu
[1] 1.089482R로 계산한 공정능력 분석 내역이다. 미니탭과 동일한 결과이다.
이때 표준편차 추정 방법 등의 옵션을 동일하게 사용해야 동일한 값을 얻을 수 있다.
Python으로 분석
아래 코드는 gpt에 공정 능력 계산 하는 방법 질문후, 한쪽 규격만 넣을 경우에 자동으로 판정하여 계산하는 logic으로 보완하여 구현하였다.
링크 코드 Colab에서 실행 할 수 있다.
미니탭, R과 동일한 값을 보여준다. 그리고 아래는 이상치를 제거한 후의 공정능력이다.
이상치 제거 전 공정 능력은 ‘Mean’: 30.2467, ‘Cpu’: 1.2899, ‘Ppu’: 1.0895
이상치 제거 후 공정 능력은 ‘Mean’: 30.3655, ‘Cpu’: 1.2795, ‘Ppu’: 1.4729 으로
단기 공정 능력은 조금 낮아졌으나, 장기 공정 능력은 향상된 것을 확인할 수 있다.
서두에서 언급한 이상치 데이터를 제외하고 공정능력을 파악하는 기능은 미니탭, R 프로그램에는 없고, 수작업으로 데이터를 삭제하고 계산 해야 한다.
파이썬으로 구현하면 쉽게 계산 할 수 있는 것이다.
코드 주요 내용
from google.colab import files
import pandas as pd
import numpy as np
import io
# 파일 업로드
uploaded = files.upload()
# 업로드된 파일 이름 가져오기
filename = list(uploaded.keys())[0]
# CSV 파일 읽기
df = pd.read_csv(io.BytesIO(uploaded[filename]),index_col=0)
# 데이터 전체 펼치기 (장기 계산을 위해)
data = df.values.flatten()
data = data[~np.isnan(data)] # NaN 제거
# 공정능력 계산 함수
def calculate_process_capability(data,USL=None, LSL=None):
# 평균 및 표준편차 계산
x_bar = np.mean(data)
print("평균 :", round(x_bar,4))
sigma_overall = np.std(data, ddof=1) # 장기 산포
print("전체 산포 :", round(sigma_overall,4))
group_std = df.std(axis=1, ddof=1)
sigma_within = group_std.mean()
print("군내 산포 :", round(sigma_within, 4))
results = {'Mean': round(x_bar, 4)}
if USL is not None and LSL is not None:
Cp = (USL - LSL) / (6 * sigma_within)
Cpk = min((USL - x_bar), (x_bar - LSL)) / (3 * sigma_within)
Pp = (USL - LSL) / (6 * sigma_overall)
Ppk = min((USL - x_bar), (x_bar - LSL)) / (3 * sigma_overall)
results.update({
'Cp': round(Cp, 4),
'Cpk': round(Cpk, 4),
'Pp': round(Pp, 4),
'Ppk': round(Ppk, 4)
})
elif USL is not None:
Cpu = (USL - x_bar) / (3 * sigma_within)
Ppu = (USL - x_bar) / (3 * sigma_overall)
results.update({
'Cpu': round(Cpu, 4),
'Ppu': round(Ppu, 4)
})
elif LSL is not None:
Cpl = (x_bar - LSL) / (3 * sigma_within)
Ppl = (x_bar - LSL) / (3 * sigma_overall)
results.update({
'Cpl': round(Cpl, 4),
'Ppl': round(Ppl, 4)
})
else:
result = " USL, LSL 한개라도 입력되어야 합니다. 다시 시도하세요"
# 숫자만 출력하기 (float로 변환)
clean_result = {k: float(v) for k, v in results.items()}
return clean_result
data_cp = calculate_process_capability(data, USL=45, LSL=None)
print(data_cp)
# 위 코드에서 3s 밖의 이상치를 제거하고 공정능력 계산하는 Logic
def remove_outliers_3sigma(data):
"""3시그마 방식으로 이상치 제거"""
mean = np.mean(data)
std = np.std(data, ddof=1)
lower_bound = mean - 3 * std
upper_bound = mean + 3 * std
return data[(data >= lower_bound) & (data <= upper_bound)]
removeData = remove_outliers_3sigma(data)
newCp =calculate_process_capability(removeData, USL=45, LSL=None)
print("이상치 제거 공정능력 : ", newCp)
# 이미지로 전체 산포 보기
# 히스토그램 시각화
from scipy.stats import norm
import matplotlib.pyplot as plt
def plot_histogram_with_distribution(data=data, USL=None, LSL=None):
x_bar = np.mean(data)
sigma = np.std(data, ddof=1)
# 히스토그램
plt.hist(data, bins=20, density=True, alpha=0.6, color='skyblue', edgecolor='black', label='Histogram')
# 정규 분포 곡선
x = np.linspace(min(data), max(data), 100)
plt.plot(x, norm.pdf(x, x_bar, sigma), 'r-', lw=2, label='Normal Dist.')
# 평균선
plt.axvline(x_bar, color='blue', linestyle='--', label=f'Mean = {x_bar:.2f}')
# USL / LSL 선
if USL is not None:
plt.axvline(USL, color='red', linestyle='--', label=f'USL = {USL}')
if LSL is not None:
plt.axvline(LSL, color='green', linestyle='--', label=f'LSL = {LSL}')
plt.title('Process Capability Histogram')
plt.xlabel('Measurement')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
plot_histogram_with_distribution(data, USL=45, LSL=None)
plot_histogram_with_distribution((removeData, USL=45, LSL=None)
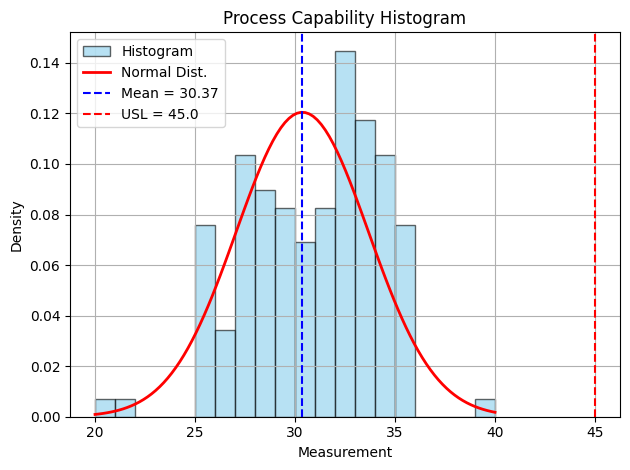
출력한 이미지는 다음과 같다.
이상치 제거 전 공정 능력산포 그래프

이상치 제거 후 공정능력 산포 50 발생 건이 삭제 되었다.
공정 능력의 개선
공정 능력 개선 하는 전 먼저 공정이 안정된 상태이어야 한다는 것이다. 이상 원인에 의한 변동이 많이 일어 나는 공정에서의 공정 능력 관리는 무의미 한다. 먼저 이상 원인이 발생 하지 않도록 5M +1E 요소가 안정적으로 관리되어야 한다.
공정 능력을 개선하기 위해서는 프로세스의 과도하게 설정된 목표치를 변경하거나, 프로세스 고유의 변동을 감소시킬 필요가 있다.
그러나 과도하게 설정된 Spec이란 고객 요구 사항이거나, 다른 부품과의 조합 등 다른 문제를 발생시킬 수 있기에 신중하게 접근해야 한다.
변동(산포)를 개선 하기 위해서는 단순화, 표준화, 실수방지, 설비 개선, 자동화 등의 작업이 필요하다.
이러한 활동도 파레토챠트 분석, 특성 요인도로 주요 특성의 추출, 해당 특성을 개선 하였을 때 실질적 산포를 줄일 수 있는지 개선 전후와 다른 영향이 없는지 확인해야 한다.
공정능력이 개선되면 검사 필요성 감소, 보증 비용 감소, 서비스 불만 감소, 생산성 증가 등 많은 이점이 있다.
일본 다꾸치(Genichi Taguchi)는 불량을 전통적인 규격을 벗어난 것이라 생각하지 않고, 목표치와의 거리로 생각하였다. 즉 목표치로 부터 벗어난 거리가 멀 수록 품질 비용이 증가한다고 보고, 손실 함수로 계산하였다. 설계 단계부터 강건한 설계를 강조하여 사회적 손실을 감소시키는 방향이라 주장하였다. 공정관리 담당자는 단순히 규격을 벗어난 것보다, 목표치와의 거리를 좁히는 것에 촛점을 맞추어 개선해야 할 것이다.
관리도와 마찬가지로 각 프로그램을 활용해 공정능력을 산출해 보았다. 공정능력은 실시간으로 파악하기보다는 일정량의 데이터가 누적된 후 계산하는 경우가 많아, 개별 프로그램으로도 계산이 가능하다.
그러나 공정 능력은 정기적으로 산출하여 이전 항목과 비교하며, 공정능력이 개선되는지 확인해 볼 필요가 있다. 그렇게 하려면 수많은 공정과 부품의 공정능력을 확인하고 비교하는 작업은 상당한 수작업과 시간이 필요하게 되므로, 파이썬으로 자동화해두면 보다 효율적으로 관리할 수 있을 것이다.